Bayes’ theorem produces A/(A+B+C), where A, B, and C are the probabilities that various hypotheses are true given that you observed an event. But I find it nicer to deal with A:B:C directly. The point that ratios are more intuitive is not original, but I wanted to write my own post explaining the theorem in terms of ratios.
Say that my acquaintance who usually comes to my events declines an invitation to dinner, saying they’re booked that night. I made a great fool of myself around them last week, so I wonder if they’re free but are pretending not to be. Due to their repulsion.
I know the friend is busy every third night on average. This provides my prior belief – 1/3 chance that they have a real conflict, 2/3 chance that they’re free. Now I apply the knowledge to generate my new belief about whether they had a real conflict or not.
- Prior belief they had a real calendar conflict: 0.33
- How likely is it they’d decline if they had a conflict? Very likely. But not 100%. I’ve known them to ditch events when better opportunities came up. Dinner at my house is a middling event, and they’ve probably cooled on me, so there’s only a 4% chance they’d cancel preexisting plans for it.
- You know this scenario is hypothetical because I don’t have my shit together enough to host dinners for my social circle. I aspire to worry about this one day!
So, in the 33% of universes (gray bar) where they have a conflict, 96% of the universes would look like the one I’m in now (blue bar). Which makes for a universe-share of 0.33 x 0.96 = 0.32.
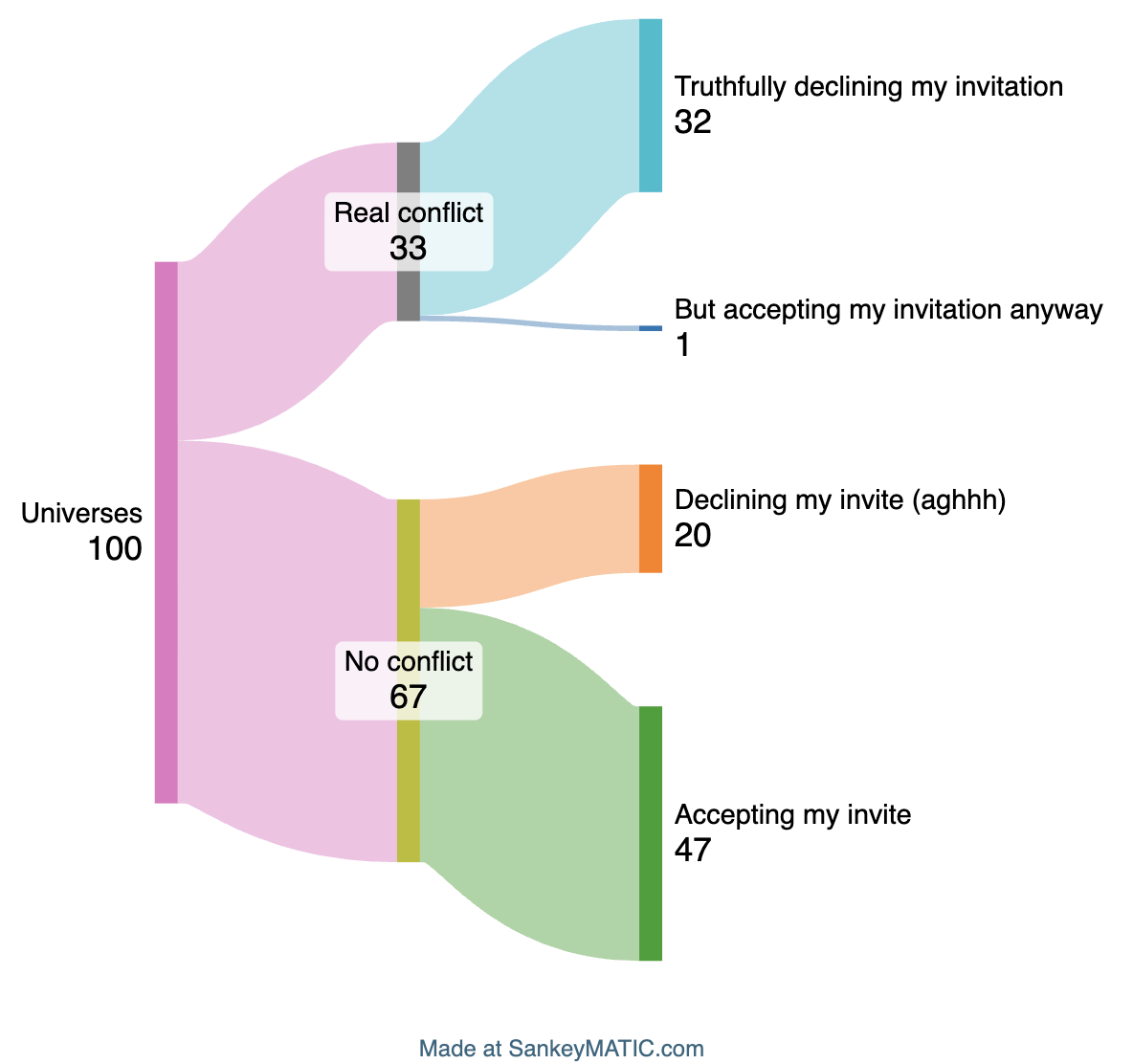
- Prior belief they did not have a conflict: 0.67
- How likely is it they’d decline even if they didn’t have a conflict? Maybe 0.3. I was a great honking fool last week.
So, in the 67% of the universes where they didn’t have a calendar conflict (chartreuse bar), 30% of those universes would look like the one I’m in now (orange bar). Which makes for a universe-share of 0.67 x 0.3 = 0.2.
I know I don’t live in the universes where they accepted the invite, so it’s a question of whether I’m in one of the 0.32 blue universes or in one of the 0.2 orange universes.
I find this slightly nicer than trying to jump straight to the figure 0.2/(0.2+0.32), which Bayes’ theorem is designed to do.
